Simplicial sets are useful for… okay, I really have no idea what. I just got sucked into reading about them. Of many available references, I enthusiastically recommend Friedman’s notes; the quality of exposition is totally unparalleled. The following are merely my notes on the differences between simplicial complexes, delta complexes, and simplicial sets.
Complexes

So you want to jam simplices together to make shapes. Maybe you’re building a 3-D model out of triangles for a video game. Because we attempt to understand things via their sub-things, the following assumptions are convenient, and thus shared by all the complexes we’re about to discuss:
- Each simplex comes with all its sub-simplices (itself, faces, vertices, etc), and
- The intersection of simplices is always a union of their sub-simplices.
Simplicial complexes
To recover the definition of a simplicial complex, just require:
- Additional assumption for simplicial complexes
- Each simplex can be specified uniquely by the set of its vertices.
This is a union of simplices in the nicest way possible; and video game model formats such as MD2 actually specify their simplices as lists of vertices.
Delta complexes
Sometimes you want to do more than play video games. It being May, maybe you wanted to pick some flowers.
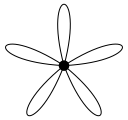
This is still made of simplices (a point and some (curved) line segments); but a set of vertices no longer determines the simplex. We attempt a generalization:
- Delta complex data model
- For each simplex, list not just the 0-subsimplices, but all the subsimplices.
Then the above flower can be specified with the following information:
- a point \(P\);
- five line segments \(a\), \(b\), \(c\), \(d\), and \(e\); and
- the left endpoint of \(a\) is \(P\) and so is the right endpoint;
- …and similarly for the other four line segments.
Organizing the delta complex data model
Data needed to describe the flower above
- A set of 0-simplices (points)
- A set of 1-simplices (line segments)
- A “left endpoint function” taking 1-simplices to 0-simplices
- A “right endpoint function”, similarly
In higher dimensions
From the 2-simplices we’d need 3 edge maps and 3 vertex maps, along with some compatibility conditions like how some vertices of some edges are vertices of some other edges—in other words, the subsimplex functions have to compose the same way they do in a typical simplex. If we call that a “reference simplex” and encode it as a category \(\widehat{\Delta}^{\mathrm{op}}\) that looks like this:
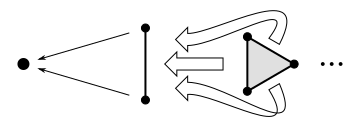
…then we can define a delta complex to be a functor from \(\widehat{\Delta}^{\mathrm{op}}\) to the category of sets.
Recovering the usual definition of \(\widehat{\Delta}\)
A subsimplex of the reference simplex is determined by the set of its vertices; so the arrows in \(\widehat{\Delta}^{\mathrm{op}}\) can be expressed by reversing inclusions of sets of vertices. Then it’s just a matter of realizing that we can make there be exactly one arrow per face inclusion by ordering the vertices and requiring the set inclusions to be increasing functions.
Simplicial sets

To go from Delta complexes to simplicial sets is to allow “degenerate simplices”—simplices that have secretly collapsed down to a lower dimension. This is encoded as a category \(\Delta\), obtained from \(\widehat{\Delta}\) by replacing “increasing” with “nondecreasing”. Significant consequences of this minor-looking change include:
-
Every simplex now comes with all its possible degeneracies. So that nice triangle mesh from your favorite video game becomes full of squashed 3-simplices and 4-simplices and 5-simplices and…
-
On the bright side, those degenerate simplices make it possible to define products of simplicial sets in a way that looks too good to be true. A good picture of why it works is in Chapter 5 of Friedman’s notes; but I have to leave it to you to come up with a pithy colloquial explanation that you personally find satisfying.
- Exercise
- As simplicial sets, how does the flower in Figure 2 differ from a point? (That is, what property of the degeneracy function from 0-simplices to 1-simplices distinguishes them?)
What’s still missing
Geometry textbooks are full of wacky instructions like “glue this face to that face with an \(x\)-degree twist”; but there’s no freedom to do so on the faces of a simplex—each face comes with an ordering of its vertices, which determines the only way they can be glued together. Even degeneracies don’t help, owing to the “nondecreasing” condition.
Really, we shouldn’t expect simplicial sets to allow arbitrary reordering when gluing faces together. That would allow gluing a face of a face to itself with arbitrary reordering—which amounts to taking a quotient by some subgroup of permutations of vertices. If you need that kind of flexibility, it’s probably time to invoke good ol’ barycentric subdivision.
