This post was originally a talk given in Pizza Seminar on October 15, 2014. Most of the mathematical content is from Wikipedia and this paper by Niizeki.
Abstract
The crystallographic restriction theorem says a finite-order automorphism of \(\mathbb{Z}^3\) (in chemistry language, a symmetry of a crystal) has order 1, 2, 3, 4, or 6. But \(\mathbb{Z}^3\) is small potatoes; so let’s go to \(\mathbb{Z}^n\), do some Galois theory in cyclotomic fields, and get us some icosahedral symmetry! (Icosahedrite is a real thing, say serious scientists.) Pretty pictures will be provided, including demonstrations of self-similarity. Self-similarity is always cool, right?
Contents
- Abstract
- Contents
- The crystallographic restriction theorem
- X-ray crystallography: peeking inside real crystals
- Slicing higher-dimensional lattices
- Self-similarity
- 3-D quasicrystals
- Footnotes
The crystallographic restriction theorem
A crystal is a regular grid (like \(\mathbb{Z}^3\)) of atoms. There is a remarkable theorem about what symmetries a crystal can admit:
- Theorem (crystallographic restriction theorem)
- If \(A \in \operatorname{Aut} \mathbb{Z}^3\) has finite order, then the order is 1, 2, 3, 4, or 6.
- Proof
- Properties of \(A\) imply properties of its eigenvalues:
\(A\) eigenvalues finite order on the unit circle \(S^1\) real in complex conjugate pairs (so one is \(\pm 1\)) integer their sum, \(\operatorname{tr} A\), is an integer So if \(e^{i\theta}\) is an eigenvalue of \(A\), then \[ \operatorname{tr} A = e^{i\theta} + e^{-i\theta} \pm 1 = 2 \cos \theta \pm 1. \] Therefore \(\cos \theta \in \frac{1}{2} \mathbb{Z}\). The eigenvalues \(e^{i\theta}\) satisfying this are of order 1, 2, 3, 4, and 6.
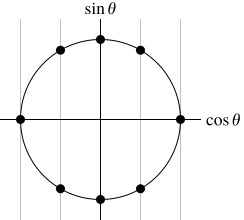
Eigenvalues on the unit circle with half-integer real part
X-ray crystallography: peeking inside real crystals
Setup
Here’s how scientists figure out the internal structure of a crystal. To start, shine an x-ray on it and record the scattered radiation on film. For our purposes, an x-ray is a function \(f\) satisfying \[ f(x+?) = e^{i k \cdot x} f(?) \] for some vector \(k\) that depends on the ray direction and wavelength. This lets us calculate the factors by which \(f\) changes from source \(x_1\) to atom \(x\) and from atom to film \(x_2\).
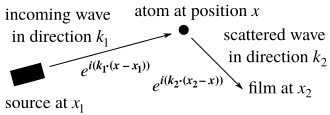
The total change in \(f\) is by a factor of \( e^{i[(k_1 - k_2) \cdot x - k_1 \cdot x_1 + k_2 \cdot x_2]} . \) Integrating this over all atom positions \(x\) in the crystal yields the total radiation bounced in the direction of \(k_2\). So…
- Upshot
- The photo records (part of) the Fourier transform of the distribution of atoms.1
A troublesome photo
Since rotational symmetries of a lattice are inherited by its Fourier transform, photos like the one below would seem to violate the crystallographic restriction theorem.

by Materialscientist on Wikimedia Commons (CC-BY-SA-3.0)
Demo: Making waves
To get a picture of what kind of crystal we’re looking at, let’s approximate the inverse transform by adding waves at \(n\) regularly spaced angles. Try it for 5, 8, 12, and 7.
You can animate these too; and Jason Davies has a WebGL adaptation of the animation.
Slicing higher-dimensional lattices
The problem: locating atoms
The last demo showed you the graph of \(f(x) = \displaystyle\sum_{i=1}^n \cos (k_i \cdot x) \) in \(\mathbb{R}^2\) for evenly spaced \(k_i\) on the unit circle. This is all very nice and smooth, but we want to actually place atoms—discrete points—in a grid. Let’s put them in the hotspots—i.e. where \(f\) hits some threshold.
To turn this into a discrete process, use the following trick: realize the waves \(\cos (k_i \cdot x)\) as 2-D slices of independent waves in \(\mathbb{R}^n\)—then hotspots are where the slice passes near lattice points.
The explicit recipe
Let \(f\) be the restriction of the function \[ \mathbb{R}^n \ni x \mapsto \sum_{i=1}^n \cos (e_i \cdot x) \] to a 2-plane on which the basis vectors \(e_i\) project to \(k_i\). To choose the 2-plane, let \(A \in \operatorname{GL}_n \mathbb{Z}\) act by cycling the basis vectors \(e_i\). Diagonalizing over \(\mathbb{C}\) gets you the matrix \[ \begin{pmatrix} \zeta & & & & \\ & \zeta^{-1} & & & \\ & & \zeta^2 & & \\ & & & \zeta^{-2} & \\ & & & & \ddots \end{pmatrix} \] where \(\zeta = e^{2 \pi i / n}\). Over \(\mathbb{R}\), the eigenvalues pair into 2×2 blocks, corresponding to 2-planes on which \(A\) acts as rotation by a multiple of \(\frac{2\pi}{n}\). Pick any one of them.
- Upshot
-
- The 2-plane is a 2-dimensional subrepresentation \(V\) of \(\langle A \rangle \curvearrowright \mathbb{R}^n\).
- Atoms (hotspots) are points of \(V\) that lie kinda near points of \(\mathbb{Z}^n\).
Demo: Atoms in 2-D quasicrystals
With this in hand, a computer can be convinced2 to find the atoms for you, drawing larger dots for better hotspots. Try it for several values of \(n\); I suggest 5, 7, 8, 6, 2, 12, and 11.
- Remark
- An alternative method is to slice fundamental domains (\(n\)-cubes) with the 2-plane, which yields pictures like the Penrose tiling below. Jason Davies has an applet you can play with, based on an older one by Greg Egan.

by Inductiveload on Wikimedia Commons (PD)
Self-similarity
At this point, we could go home—we have a description of quasicrystals from which we can produce both interactive computer renderings and theorems (like quasicrystals not actually having translational symmetry, due to \(V\) containing no integer points besides 0).
Of course, there is more—the “quasi”-ness of quasicrystals allows a sort of self-similarity that honest crystals can’t have. To see it in action, go back to that atoms demo and try zooming in or out for a while.
To explain this self-similarity—the apparent indistinguishability of different zoom levels—we will need a bit of number theory.
A number-theoretic model of quasicrystals
- Theorem (crystallographic restriction in arbitrary dimensions)
- \(\operatorname{GL}_m \mathbb{Z} \) contains a matrix \(A\) which has \(\zeta_n = e^{2\pi i/n}\) as an eigenvalue (so it rotates some 2-plane by \(\frac{2 \pi}{n}\)) if and only if \(m \geq \varphi(n)\), where \(\varphi\) is Euler’s totient function.
- Proof
- The Galois conjugates of \(\zeta_n\) must also be eigenvalues
of \(A\).
- Since \(\zeta_n^n = 1\), they’re \(n\)th roots of 1.
- Since \(\zeta_n\) generates all \(n\)th roots of 1, they’re primitive—i.e. \(\zeta_n^k\) where \(k\) and \(n\) are coprime.
The number of such \(k\) is \(\varphi(n)\). To prove that \(\varphi(n)\) works, observe that \[ \mathbb{Z}[\zeta_n] \hookrightarrow \mathbb{Q}(\zeta_n) \cong_{\mathbb{Q}\text{-vect}} \mathbb{Q}^{\varphi(n)} \subset \mathbb{R}^{\varphi(n)} \] as a discrete subgroup, since the field norms of the leftmost terms are in \(\mathbb{Z}\).
- Remark
- If \(p\) and \(q\) are large enough primes, you can produce an integer matrix \(A\) of order \(pq\) and size \(\varphi(p) + \varphi(q) < \varphi(pq)\), but it won’t rotate any 2-plane by \(\frac{2\pi}{pq}\).
A mathematical description of zooming
Here’s how we implement3 zooming: scale the 2-plane \(V\) by some factor and the unseen \(m-2\) dimensions by some other factor to preserve \(m\)-dimensional volume. That way the total visual density of dots remains about the same. Here’s how we interpret zooming and self-similarity:
- Zooming acts by scalars on \(V\) and the other irreducible sub-representations of \(\langle A \rangle \curvearrowright \mathbb{R}^{\varphi(n)}\), so zooming is a 1-parameter subgroup \(\gamma\) in \(\operatorname{SAut}_A \mathbb{R}^{\varphi(n)} \) (volume preserving automorphisms).
- Visually, transforming by anything in \(\operatorname{Aut} \mathbb{Z}[\zeta_n]\) isn’t detectable.
- Self-similarity means that the image of \(\gamma\) in \(\operatorname{SAut}_A \mathbb{R}^{\varphi(n)} / \operatorname{Aut} \mathbb{Z}[\zeta_n]\) accumulates on itself (or is periodic).
The existence of self-similarity rests on one key fact from number theory.
- Theorem (Dirichlet’s Unit Theorem)
- Suppose a number field has \(r\) embeddings in \(\mathbb{R}\) and \(c\) embeddings in \(\mathbb{C}\). Then its group of units has rank \[ r + \frac{c}{2} - 1 . \]
- Corollary
- \(\operatorname{SAut}_A \mathbb{R}^{\varphi(n)} / \operatorname{Aut} \mathbb{Z}[\zeta_n]\) is compact.
- Proof
- Since automorphisms act by scalars on all irreducible subrepresentations,
\[\begin{align*} \operatorname{Aut}_A \mathbb{R}^{\varphi(n)} &\cong (\mathbb{C}^\times)^{\frac{\varphi(n)}{2}} \cong (\mathbb{R} \times S^1)^{\frac{\varphi(n)}{2}} \\ \operatorname{SAut}_A \mathbb{R}^{\varphi(n)} &\cong \mathbb{R}^{\frac{\varphi(n)}{2} - 1} \times (S^1)^{\frac{\varphi(n)}{2}} . \end{align*}\]
Since \(\mathbb{Z}[\zeta_n] = \mathcal{O}_{\mathbb{Q}(\zeta_n)}\), Dirichlet’s Unit Theorem implies that \(\operatorname{Aut} \mathbb{Z}[\zeta_n]\) contains a copy of \(\mathbb{Z}^{\frac{\varphi(n)}{2} - 1}\). Then \(\operatorname{Aut} \mathbb{Z}[\zeta_n]\), being discrete (it’s conjugate to a subgroup of \(\operatorname{SL}(\varphi(n), \mathbb{Z})\)), is cocompact.
Self-similarity now follows, having been reduced to the statement that a 1-parameter subgroup of a torus is recurrent.
- Remark
- The image of \(\gamma\) is periodic when (and only when) \(\varphi(n) = 2\)—so when \(n\) is 5, 8, 10, or 12. This makes the self-similarity exact—i.e. different zoom levels can look identical (not just suspiciously similar)—and allows one to build games like Richard Schwartz’s Lucy and Lily based on facts like \[ (2 + \sqrt{5})(2 - \sqrt{5}) = -1. \]
- Remark
- Michael Rule’s collection of quasicrystals graphics includes an alternative description of zooming that sidesteps the number theory, instead using Shepard Tones to produce self-similarity.
3-D quasicrystals
The n-dimensional viewpoint
A quasicrystal with irreducible symmetry \(G\) is an irreducible-over-\(\mathbb{R}\) subrepresentation \(V\) of an irreducible-over-\(\mathbb{Z}\) representation \(G \hookrightarrow \operatorname{SL}(m,\mathbb{Z})\). The atoms are points of \(\mathbb{Z}^m\) near \(V\), and the Galois conjugates of \(V\) (the other subrepresentations over \(\mathbb{R}\)) allow the possibility for self-similarity.
The search for 3-D quasicrystals
To look for 3-dimensional quasicrystals, one first finds a list of the seven irreducible finite subgroups of \(\operatorname{SL}(3,\mathbb{R})\). Most of these preserve an ordinary 3-D lattice—i.e. the representation can be defined over \(\mathbb{Z}\). The two exceptions are the two icosahedral groups—the alternating group \(A_5\) and the product \(A_5 \times \{\pm 1\}\)—so up to finite index subgroups, there’s only one irreducible 3-D quasicrystal, which you can explore in the following demo.
The standard representation of \(A_5\) has one Galois conjugate, which can be found in a list of representations of \(A_5\). The two representations can be described explicitly as follows: in the standard representation, \(A_5\) acts by rotation on the icosahedron with vertices \(\pm(\sqrt{5}, 0)\) and \(\pm(1, 2\zeta_5^k)\) in \(\mathbb{R} \times \mathbb{C}\). To obtain the other representation, merely conjugate the action on the set of vertices by the permutation induced by \(\zeta_5 \mapsto \zeta_5^2\).
Oh, and—yes, they’re real.

by AMES Lab., US DoE via Wikimedia Commons (PD)
Footnotes
-
The photo loses phase information, the recovery of which is a nontrivial problem. ↩
-
For efficiency reasons, the demo actually uses the number-theoretic model from the section after. ↩
-
Self-similarity is what makes zooming possible (i.e. not unbearably slow) in the atoms demo—the atom finder can get away with exploring a 2-dimensional slice instead of the entire \(m\)-dimensional space. ↩